Hazel and I LOVE Disney's movie Frozen. We are constantly listening to the soundtrack in our car. One of our favorite songs from the movie is Let It Go. If you have not heard the song or seen the movie you can check out the song from the actual movie (with movie scenes) from Disney's website.
Disney's Frozen "Let It Go" Sequence Performed by Idina Menzel on Disney Video
Now there are many wonderful lessons in the movie for both children and adults, but that is for another post. Hazel has decided that Frozen is a possible theme for her birthday party, so I have been pinning many sources. Often I see Frozen Fractals referred to in either food or craft and it makes me cringe. I spent a week for three summers in New Haven, Connecticut taking classes on fractals and I have to share some of my knowledge as well as some lessons with you.
Let's start with some terms. First the word "fractal" was coined by Benoit Mandelbrot in the 1970's. And yes that is me in the picture with Benoit Mandelbrot. Every year he came to lecture at the class one of the days. I have even met his wife and eaten lunch with her. Mandelbrot noticed that several things he was looking at had similarities others had not noticed before. He decided to classify this group of things with the same characteristics fractals. The things he was looking at included how often computers make mistakes when they talk to one another, how jagged coastlines are, how much it rains in different parts of a rainstorm, how money moves on the stock market and how the galaxies are spread across the universe. The similarity he discovered was that they are all made up of little parts that look like the whole thing. So shapes that are made up of little parts that look like the whole thing are called fractals. We call this characteristic self-similarity. (For examples of self-similarity check out Yale's wonderful site on fractals and choose 1A and 1B.)
Now fractals occur in nature all the time. You can look at a tree or a piece of broccoli and see them. A great book to see them in nature is Mysterious Patterns: Finding Fractals in Nature by Sarah C. Campbell with a afterward on Benoit Mandelbrot written by Michael Frame (the Yale professor who taught the fractal courses I took and worked with Mandelbrot). I used this afterward as a source for the information shared here.
"Solkoch". Licensed under Public domain via Wikimedia Commons.
To create fractals, one must apply the same process over and over on a smaller scale. This is called iterating. An example of iterating is easy to find in some of the simple fractals. Since Queen Elsa refers to frozen fractals, we will work with the Koch Snowflake.The picture above is a more difficult one than the one we will make by hand. To start you need a piece of paper, a pencil and a ruler. To begin draw an 18 cm line segment. This is stage 0 or the initiator.
To get to Stage 2, you do the same steps as above (middle section) to each line segment in Stage 1. So now the thirds will be 2 cm. Measure all four segments and mark the thirds. Then erase the middle section of each line segment. Draw in the two 2 cm lines for each erased spot.
"Koch curve" by Fibonacci. - Own work. Licensed under CC BY-SA 3.0 via Wikimedia Commons.
Now what we have drawn is actually known as the Koch curve. The Koch snowflake starts with an equilateral triangle instead of the line segment.The snowflake iterations look like this:
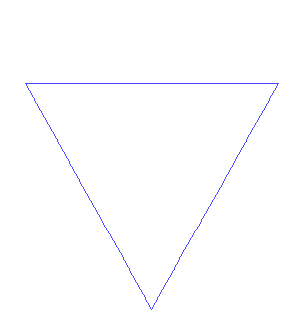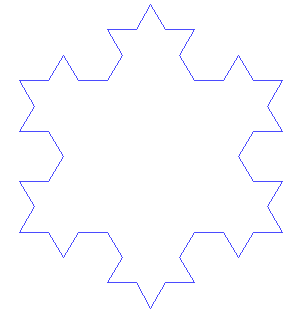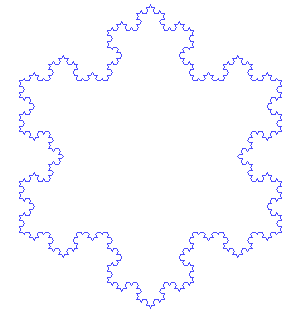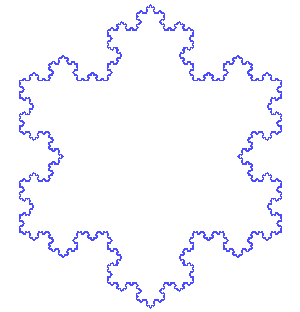
"Von Koch curve" by António Miguel de Campos - self made based in own JAVA animation. Licensed under Public domain via Wikimedia Commons.
Now fractals have an infinite number of iterations, so the perimeter of the Koch Snowflake is infinite. However it does have an area. Cynthia Lanius' Fractals Unit does a great job of explaining this and demonstrating it. It is a great lesson for working on area as well as a nice introduction to limits for older children.
Next experiment and see if you can come up with your own snowflake fractal. Be sure to send me a picture if you do! Now there are many other fractals and activities you can do with them. I will share some more with you soon. Stay tuned!!
For more math lessons and Frozen ideas check out:
